Magnetický obvod
Demagnetizace
Jak už název napovídá, jedná se o proces, při kterém se snižuje celková magnetická polarizace v magnetu. Může se tak stát působením vnějšího magnetického pole opačného směru ke směru polarizace. Tento proces se nazývá odmagnetování. Kromě toho je však každý magnet podroben působení vnitřního demagnetizačního pole Hd, jehož vznik souvisí s principem snižováním jeho vnitřní energie. Velikost Hd je dáno vztahem:
Hd = - Kd . J / µo (3)
kde Kd je demagnetizační faktor

Faktor Kd závisí na tvaru magnetu a směru magnetování a jeho přesný výpočet je v obecném případě komplikovaný. Jednoduchý vzorec platí pouze pro rotační elipsoid, který se však v praxi nevyskytuje. Proto se využívá tabulkových hodnot nebo různých matematických aproximací. Obecně platí, že čím je větší poměr rozměru magnetu ve směru magnetování vůči jeho kolmým rozměrům (někdy nazývaný poměrem štíhlosti magnetu), tím menší je jeho demagnetizační faktor. Závislost má charakter hyperboly, tj. zmenšení poměru na polovinu např. může znamenat zmenšení Kd o desetinu, ale také desetkrát.
Pracovní oblast
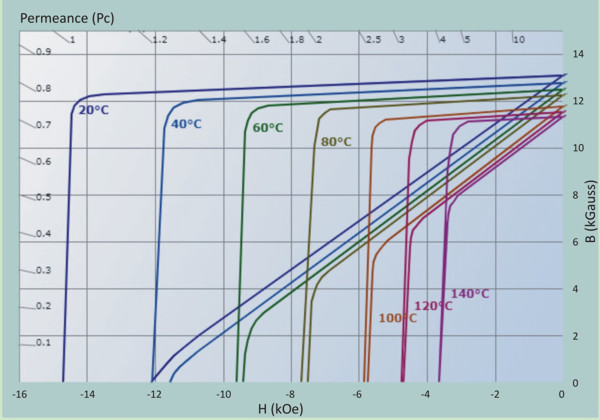
Často se místo hysterezní smyčky zobrazuje pouze druhý kvadrant této závislosti - tzv. demagnetizační křivka, která zachycuje pracovní oblast trvalého magnetu a její významné body. Pracovním bodem Pw trvalého magnetu je bod na této křivce, charakterizovaný dvojicí Bw , Hw . Díky demagnetizaci se posune pracovní bod magnetu po zmagnetování z remanence po demagnetizační křivce vlevo až do konečného bodu Pw , o jehož poloze právě rozhoduje Kd magnetu resp. celého obvodu. V optimálním případě se Pwshoduje s bodem (BH)max .
Magnetický obvod
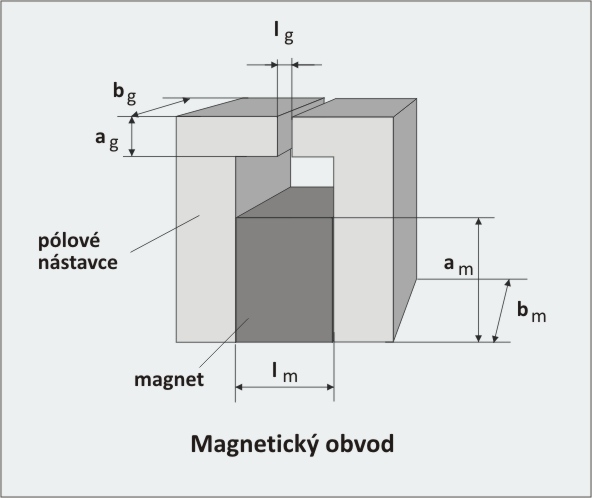 Trvalý magnet se často používá v magnetickém obvodu, složeném z magnetu a z pólových nástavců z magneticky měkkého materiálu, nejčastěji železa. Dosahuje se tím optimálního tvarování pólů a vzduchové mezery.
Trvalý magnet se často používá v magnetickém obvodu, složeném z magnetu a z pólových nástavců z magneticky měkkého materiálu, nejčastěji železa. Dosahuje se tím optimálního tvarování pólů a vzduchové mezery.
Výpočet složeného magnetického obvodu je značně komplikovaný. Vychází z aplikace Biot-Savartova zákona a zákona zachování magnetického toku. V případě obvodu na obrázku je možno výše uvedené zákony přepsat na rovnice
Hm . lm = g . Hg .lg (4)
Bm . Am = s . Bg .Ag (5)
| kde: | Hm, Bm je intenzita pole resp. indukce v magnetu |
| lm, Am je délka resp. průřez magnetu | |
| Hg, Bg je intenzita pole resp. indukce v mezeře | |
| lg, Ag je délka resp. průřez mezery | |
| g je koeficient reluktance | |
| s je koeficient úniku |
Koeficient g vyjadřuje magnetický odpor všech magneticky měkkých a nemagnetických částí obvodu (např. styčných ploch). V případě kvalitního obvodu se jeho hodnota blíží 1. Pro určení koeficientu s , který vyjadřuje míru úniku magnetického toku z mezery, nejsou k dispozici přesné analytické metody výpočtu. Zpravidla se postupuje numerickými metodami, při kterých se obvod rozdělí na množství oblastí s různými pracovními body.